CMU 15445

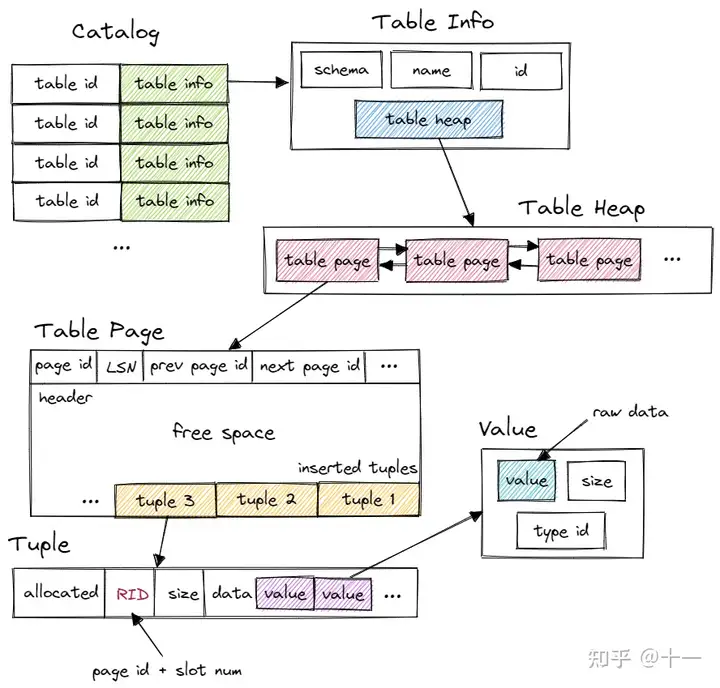
内存缓冲池

原理

存储管理器中实现缓冲池。缓冲池负责将物理页面从磁盘中读入内存、或从内存中写回磁盘，使得DBMS可以支持大于内存大小的存储容量。页面读入缓冲池时，从free-list（空位页面）后lru_replacer中（未被访问的可替换页面）寻找空间，淘汰的dirty-page还需写回磁盘，page_table映射page到frame的关系

并行缓冲池的思想是分配多个独立的缓冲池，并将不同的页面ID映射至各自的缓冲池中，从而减少整体缓冲池的锁粒度，以增加并行性。负载均衡：采用轮转方法选取分配物理页面时使用的缓冲池，start_idx++

为什么不用 OS 磁盘管理模块

OS 的磁盘管理模块没有 DBMS 中的领域知识，无法恰当地决定数据移动的时机和数量

• 将 dirty pages 按正确地顺序写到磁盘
• 定制化缓存置换策略
• 根据具体情况预获取数据

淘汰算法

LRU-K：最近使用过1次 —> 最近使用过K次，降低了“缓存污染”问题，命中率比LRU高

需要保存每个页面的访问次数、最近K次时间戳，用两个队列按顺序记录这些页面，优先淘汰访问次数不足K的

• 历史队列：访问小于k次的页面，按FIFO存放，每次访问将页面计数++，满k次放入缓存队列
• 缓存队列：访问满k次的页面，按照前第K次时间排序，用SET结构存放

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

struct cmp{
    bool operator()(const pair<int, int>& a,const pair<int, int>& b) const{
        return a.second < b.second;
    }
};
//历史队列
list<int> hist;
unordered_map<int, list<int>::iterator> hist_map;
//缓存队列
set<pair<int, int>> cache;
unordered_map<int, set<pair<int,int>>::iterator> cache_map;
//页面时间戳与访问次数
unordered_map<int, list<int>> timestamp;
unordered_map<int, int> count;

void record(int id){
    count[id]++;
    timestamp[id].push_back(TIME++);
    int cnt = count[id];
    if (cnt == 1) {
        hist.push_back(id);
        hist_map[id] = --hist.end();
    } else if (cnt == 2) {
        hist.erase(hist_map[id]);
        hist_map.erase(id);
        int k_time = timestamp[id].front();
        auto it = cache.insert({id, k_time});
        cache_map[id] = it.first;
    } else {
        timestamp[id].erase(timestamp[id].begin());
        cache.erase(cache_map[id]);
        int k_time = timestamp[id].front();
        auto it = cache.insert({id, k_time});
        cache_map[id] = it.first;
    }
}
bool evict(int &id) {
    if (hist.empty() && cache.empty()) return false;
    if (hist.size()) {
        auto it = hist.begin();
        id = *it;
        count.erase(id);
        timestamp.erase(id);
        hist.erase(it);
        hist_map.erase(id);
    } else {
        auto it = cache.begin();;
        id = it->first;
        count.erase(id);
        timestamp.erase(id);
        cache.erase(it);
        cache_map.erase(id);
    }
    return true;
}

可扩展哈希

原理

通常的哈希表如Redis在负载因子高时，把HashTable大小翻倍，HashNode全部rehash一遍

可扩展哈希表是一种动态哈希表，其思想在于多个目录项对应一个桶，其特点为桶在充满或清空时可以桶为单位进行桶分裂或合并，并且仅需在特定情况下进行HashTable的扩展和收缩，以减小扩展和收缩操作对全表的影响

映射关系：key->index 的逻辑是hash(key) & mask，即64位hash的低k位，hashTable大小为 $2^k$。

哈希表的扩展：

1. 对于大小为 4 的 HashTable，第一次扩展时，必须把HashTable reserve 为8。此后的key hash映射因为mask了低 k+1 位，如果是 Bucket[0] 链表满了，那么rehash到 Bucket[0] 和 Bucket[4] 链表，但 Bucket[1~3] 因为不满就无需rehash，把指针赋值给 Bucket[5~7] 即可，即两个 Bucket_idx 对应相同的链表。

2. 等下次 Bucket[1] 链表满需要扩展时，因为下标1和5共用这一个链表，只需要rehash成两个链表分别对应两个Bucket_idx即可，其他都不用动

如何区分以上两种情况：

• 全局深度：HashTable的大小，即mask位数，每次reserve时+1
• 局部深度：每次rehash链表时，对应Bucket的局部深度++。局部深度 < 全局深度 时，仅需rehash对应链表节点。局部深度 = 全局深度时，需要先 reserve 再 rehash 对应链表。

桶的合并：满足两桶均空、局部深度相同时，合并桶后局部深度-1，合并后可能缩减全局深度

并发控制

• Getvalue：哈希目录加读锁

• Insert/Remove：Bucket一定会插入或分裂，但 HashTable 只有在桶满分裂时才修改，故采用乐观锁优化：默认 HashTable 只加读锁，Bucket 加写锁；只有桶满时，释放锁并调用另一分裂插入函数，一开始就获取两个写锁，还要注意判断桶是否仍满

B+Tree 索引

• TREE_PAGE: 保存在Page的data中，共4KB，包含size、max_size、parent_page_id、page_id
• TREE_INTERNAL_PAGE: kv数组 <keyType, page_id>
• TREE_LEAF_PAGE: next_page_id 与 kv数组 <keyType, record_id>

定义

参考链接

• B+树分为内部结点和叶子结点，根结点既可以是内部结点，也可以是叶子结点，关键字个数最少1个
• B+树内部结点不保存数据，只用于索引，所有数据都保存在叶结点中
• m阶B+树内部结点最多有m-1个关键字、m个子树，叶子结点最多存储m-1个记录
• 内部结点中的key都按照从小到大的顺序排列，key左子树中的key都小于等于右子树中的key
• 叶子结点双向链表相连，自小而大有序

插入

理论上B+树内部结点是由指针、关键字交替组成的，实现是一个键值对数组<key, page_id>。所以M阶的B+树内部结点最多存放M个键值对，第一个键值对键是空的，而叶子结点键值对个数为 M-1

1. 如果是空树，创建一个叶节点作为根。更新root_page_id ，因为需要通过它访问B+树
2. 从根节点向下查找到键值应该所在的叶节点，在每个内部节点找到最后一个小于等于插入值的键，得到下层结点的 Page_id，最终找到叶子结点并插入键值对。规定不支持重复键，否则直接返回 false。
3. 如果叶节点插入后超过 M-1 要进行分裂，将原节点的一半内容拷贝到新节点，分裂点的键插入父节点，让父节点该键的值指向新的叶节点
4. 如果父节点（内部节点）插入后超过了M，同样要递归进行分裂并向上插入，还要调整子节点的父指针指向新的内部节点。
5. 如果上溢到了根节点，则要创建一个新的根节点，使得 B+ 树长高一层

删除

下溢：内部结点 (M+1)/2，叶结点 M/2

1. 从叶节点中删除键值，如果出现下溢就进行后续处理：
2. 对于叶结点，如果兄弟节点键值对个数大于 M/2，从兄弟节点借一个键值对（左侧兄弟就借尾，右侧兄弟就借头），把兄弟节点的键上移替换父节点中的键（保证左<父<右）；如果兄弟节点不够借出，将该节点与兄弟节点合并，同时删除父节点中对应的键值。
3. 如果删除后父节点（内部节点）下溢出，仍然是借&修改或合并&删除两种方法处理，但规则与叶节点不同：借&修改时，同样把兄弟节点的键上移，但借来的是 <父节点的键,兄弟节点的值>；合并&删除时，要把父节点的键和兄弟节点的键值一块和该节点合并。
4. 如果下溢出到了根节点，而且根节点只剩下一个子节点，说明树应该减少一层，将这个子节点设为新的根。

并发控制

安全节点：插入后不上溢，删除后不下溢，读取时均安全。如果子节点安全，那么对其下面的节点做插入/删除操作引起的树结构变化最多会传递到该层，不会影响上层，所以可以放掉祖先节点的锁允许其它操作访问

读操作

子节点获取读锁后就释放父节点读锁，只需要一个 prev_page 指针解锁父节点

插入/删除操作

从根节点开始往下依次加写锁，直到安全节点才释放祖先节点的所有锁。在实现上，用 page_set 记录查找过程中加写锁的页面。

• 对于插入，page_set保存的写锁就足够了，因为新生成的兄弟结点不会被其它操作访问到
• 对于删除，需要对访问的兄弟节点上写锁，不在 page_set 中，单独释放。删除或合并页导致删除的页面记录到 deleted_page_set 中，最后调用内存池接口删除掉
• 另需一把锁保护根节点，只有根结点安全情况才能解锁，否则堵塞前后 root_page_id_ 可能变了

  瓶颈在于每次都要获取根节点写锁，优化方法：“乐观” 地假设插入/删除不会发生分裂或合并，于是只需沿路径像读取一样获取和释放读锁，最后检查叶节点是否安全：如果安全，则假设正确，只需对叶节点加写锁更新；如果不安全则假设错误，重新调用基础版算法。

事务与并发控制

LockManager

LockManager 实现了基于 2PL 的行级锁，自动为并发事务执行加锁解锁。当一个事务需要读写元组时候，根据自身的隔离级别尝试获得元组对应的读锁或写锁，并在适当的时刻将其释放。

LockManager 为每个表/行维护一个请求队列，用条件变量阻塞/唤醒请求，用 map 建立资源到队列的索引。队列按请求先后排序，记录了每个请求的事务、锁级别、是否授予等。

实现了三种隔离级别：

加锁操作：

1. 检查加锁是否兼容隔离级别：如 RR 在 shrinking 时不能加任何锁，RC 只能加读锁
2. 获取 table 对应的表级锁请求队列
3. 检查是否是升级锁操作，即队列里是否有相同的 tid，若有：
   • 是否有另一个事务尝试升级锁？通过upgrading字段判断，抛异常
   • 升级是否兼容，即升级后数据是否安全（限制越严越安全）：IS -> [S, X, IX, SIX], S -> [X, SIX], IX -> [X, SIX], SIX -> [X]
   • 释放此前持有的锁，后续把升级作为一个新的请求加入队列
4. 将锁加入请求队列：普通锁直接放到队尾，升级锁因为优先级高，应插入首个未授权的请求前
5. 后续该请求基于while循环和条件变量尝试获取锁，按 FIFO 遍历请求队列判断能否满足锁请求：
   • 获取读锁：如果当前txn已经是最早的事务，或前面都持有读锁，则授予
   • 获取写锁：只有当前txn是最早的事务才授予，否则一定冲突，被 cv.lock() 阻塞

解锁操作：

1. 找到表/元组的锁请求队列，遍历找到要解锁的txn
2. 根据隔离级别修改事务状态：
   • RR 时，事务进入 Shrinking
   • RC、RU 时，仅 X 锁释放使事务进入 Shrinking
3. cv_.notify_all() 唤醒所有阻塞在此请求队列上的事务

死锁检测

1. 构建有向图，遍历表锁和元组锁中的所有请求队列，把每对符合等待关系的事务 <a, b> 加入图的边集，a 是 waiting 请求，b 是 granted 请求。
2. 用 DFS 来进行环检测，需要记录环上的所有节点。挑选 tid 最大的事务终止，删除图中的边，唤醒阻塞的请求
3. 重复环检测直到无环为止

SQL执行器

1. SQL 语句先经过 Parser 生成一棵抽象语法树（libpg_query 库）；
2. Binder 遍历树，将关键字/标识符绑定到数据库实体上（c++类）；
3. Planner 遍历这棵树，生成初步的查询计划 Plan Tree，每个Plan结点都代表了一个操作，树中上层的Plan结点调用 next() 从下层结点取出一条数据，从而数据自底向上地流动，在根节点输出结果。
4. Optimizer 遍历 Plan Tree 进行逻辑规则，这种优化器不需要知道数据的具体内容，仅是根据预先定义好的规则修改 Plan 结点。
5. Executor 遍历查询计划树，将树上的 PlanNode 替换成对应的执行算子

Optimizer

TopN：对 Plan Tree 进行后续遍历，在遇到父节点 Limit、子节点 Sort 时，则将这两个节点替换为一个 TopN

HashJoin：

• 把 NestedLoopJoin 替换为 HashJoin
• 让小表驱动大表，减少表连接次数，调用已提供的api估计table大小，再根据大小来调整 Plan Tree 里 join 的顺序

IndexJoin：识别 B+Tree Index，默认只会为右表匹配 index，因此如果 左表有 index && 右表没有 && 等值连接，则把左右顺序替换一下，便于之后正确识别索引

谓词下推：需要把 Filter 正确下推至 Join 算子下，尽量接近叶子节点，减少数据拷贝耗时。自顶向下地改写，提取 predicate 中的所有 comparison，判断表达式的两边是否一个是 column value，一个是 const value，只有这样的 predicate 可以被下推，再将所有的 predicate 重新组合为 logic expression 生成新的 Filter，根据 column value 的 idx 来选择下推的分支

列裁剪：遇到连续的两个投影，合并为 1 个，只取上层投影所需列，其余直接抛弃

Executor

火山模型

每个算子都有 Init() 和 Next() 两个方法。Init() 对算子进行初始化工作，Next() 向下层算子请求下一条数据，返回 false 时说明下层算子已经没有剩余数据，迭代结束。

• 简单，每个 Operator 可以单独抽象实现、不需要关心其他 Operator 的逻辑
• 数据以行为单位进行处理，不利于CPU cache；且每处理一行需要调用多次next() 函数，虚函数开销大

HashJoinExecutor

使用基础哈希算法进行连接操作，其原理为将元组的连接键（即某些属性列的组合）作为哈希表的键，并使用其中一个子计划节点的元组构造哈希表。由于具有相同连接键的元组一定具有相同的哈希键值，因此另一个子计划节点中的元组仅需在该元组映射的桶中寻找可与其连接的元组

用unordered_multimap直接存放等于连接键的元组，再用右子节点的元组作为”探针”寻找与其连接键相同的左子计划节点的元组，可能有多个左子结点对应

AggregationExecutor

用哈希表将所有聚合键（即元组的属性列组合）相同的元组映射在一起，以此统计所有聚合键元组的聚合信息

并发控制

将 transaction 应用到之前实现的算子中，以支持并发的查询：为查询计划执行器的顺序扫描、插入、删除计划的NEXT()方法提供元组锁的保护

只需修改以下三个算子，因为其他算子获取的tuple数据均为中间结果：

1. seq_scan

   • 不同隔离级别怎么加锁？读未提交不加锁；读已提交读完 table 立即解锁；可重复读在COMMIT或ABORT后才释放锁
   • 加什么锁？表加 IS 锁，再给行加 S 锁。

     为什么不给表加 S 锁？对于 DELETE...WHERE...，同个 query 先在下层加 S 锁，又在 Delete 里加 IX，因为 S 锁不能升级 IX 锁就会卡死（整表读 -> 某行写，锁升级不兼容）

2. insert
   元组插入表时由 tablePage 锁保证并发安全，插入后为了更新索引，需要先获得元组的写锁，保证此期间元组不被修改，之后再更新索引依靠 B+tree 的锁

3. delete
   调用 next() 收到子计划节点要删除的元组后（如seq_scan），应当为该元组加写锁，然后标记元组删除，并删除索引，等到事务提交时缓冲池删除。注意在 RR 级别时，子计划节点此时拥有该元组的读锁，因此应该采用升级锁

参考链接

CMU 15-445/645
2021 CMU 15-445 实验笔记
CMU 15445 -2022通关小结
[Github] CMU15445-2021-FALL
CMU 15445 BufferPoolManager
2021 CMU-15445/645 Project #3 : Query Execution
CMU15-445 Lab3 Query Execution全记录
Concurrency Control Theory
CMU15-445 22Fall通关记录
记录一下 CMU 15445 项目
Bustub Project #2：B+ Tree（下）